〈研之有物〉電影《沙丘》的沙子是流體還是固體?談談顆粒流的物理學
顆粒體如何流動?
流沙、土石流、穀倉的米…… 這些顆粒體,究竟是如何流動的?過去,科學界對於「顆粒流」的研究起步非常晚,也一直缺乏統整型的理論。中央研究院「研之有物」專訪院內物理研究所蔡日強副研究員,他長年研究顆粒體的運動行為,實驗室透過自創的顆粒軟球實驗,試圖找到全新的方法來描述顆粒流,並為固體與流體兩個歷史悠久的學術領域,搭建出一個溝通的橋梁!
從流沙到洗米:隨處可見的「顆粒體」
「顆粒體的流動」(Granular flows)聽起來或許有點生硬,但它其實是我們生活中常見的現象,像是在廚房裡洗米、攪拌咖啡豆、或是在工地攪動砂石,都是顆粒流的一種。而如果以人類文明的發展來說,從古時候建造金字塔、到現在火星探測器的著陸,也都有顆粒流的現象參與其中。
然而,即使顆粒流與我們息息相關,科學家對它的了解卻少之有少。究竟,顆粒體是怎麼流動的?有沒有一個方程式,可以描述顆粒流的行為?中研院物理所的蔡日強副研究員,長年進行顆粒體相關研究,這一次,他希望透過全新的實驗,解開顆粒體的流動之謎!

萌芽階段的顆粒流研究
不管是固態力學或是流體力學領域,都是「百年老店」,已經累積了上百年的歷史。相較之下,顆粒流的研究非常年輕,僅僅是最近幾十年的事情而已。造成這樣的原因,除了顆粒流本身的複雜性之外,也是因為它的定位,一直處於「三不管地帶」。
顆粒流很特別,它像固體一樣,能夠堆疊、擠壓,可是又會有流動的行為,若只用固體或流體的角度切入,都很難完整描述這樣的現象。然而在學術圈,固體和流體兩大流派,經過上百年的發展,都有各自根深柢固的作法、解讀現象的方式,彼此之間存在著很大的鴻溝。
「在學術界,Solid(固體)的人講 Solid 的語言,Fluid(流體)的人講 Fluid 的語言,兩邊的溝通其實非常少!」蔡日強笑著說「我以前參加過一個應用力學大會,大會裡的會議名稱,直接分成兩種開頭,一種是 S、另一種是 F,擺明了他們討論事情的角度,不是固體就是流體。」
對顆粒流來說,這樣的二分法顯得非常尷尬。蔡日強認為,如果可以從固體與流體領域,各自吸取一些精髓,或許能夠連接兩個學派,用不一樣的角度研究顆粒流!
如何研究「顆粒體的流動」?
為了瞭解顆粒體如何流動,蔡日強設計了一套獨特的實驗方法,可以分為「顆粒體」與「容器」兩個部分。
在「顆粒體」方面,蔡日強採用醫用材料(PDMS),製作出許多顆粒軟球,硬度接近橡皮擦、大小約一公分。為什麼會採用「軟」球來代表顆粒體呢?
過去,在物理學家的理論中,常常會把顆粒體視為「剛體」。然而,剛體的假設在理論上不僅無法呈現顆粒體被壓縮的情況;而且實驗上,也很容易遇到麻煩!
如果採用剛硬的顆粒體做實驗,在緊密排列時,很容易「卡死」,不只完全動不了,也很可能讓珍貴儀器損壞。為了讓顆粒體可以緊密排列,又不會完全卡死讓儀器動不了,可以擠壓、變形的顆粒軟球,就成為了最好的實驗材質。
影片為實驗室展示用,實際操作時液體會淹沒顆粒軟球,保持液體折射率和軟球一致,以便用光學攝影機記錄內部軟球的運動情況(註 1)。資料來源│研之有物

至於在「容器」方面,蔡日強在裡面設計了齒輪狀的錐形圓盤:上方的錐形圓盤連接馬達,可以不斷旋轉;齒輪狀可以咬住顆粒軟球,帶動容器內的顆粒軟球一起轉動。
設計成錐形的用意,則是可以讓容器內的顆粒體,不論在什麼位置,切變率(shear rate)都可以維持一致。簡單來說,錐形圓盤試圖讓讓整體流動盡可能「均勻」,讓相鄰顆粒之間的速度不至於落差太大(註 2)。

每一次的實驗,錐形圓盤都會進行定速轉動(固定角速度,Ω),施以所有顆粒軟球固定的切變率。同時,研究團隊也會記錄,在馬達固定轉速時,系統需要多大的轉矩來對抗馬達。但初步實驗即出現了非常匪夷所思的現象!
匪夷所思的實驗結果
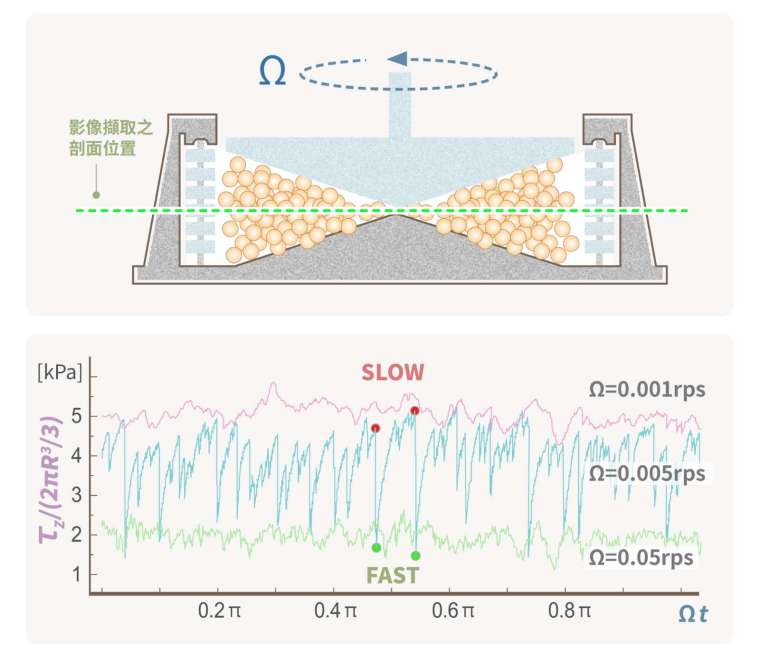
從上圖的實驗數據顯示,在低轉速時(Ω = 0.0001 rps),系統產生的轉矩最高;在高轉速時(Ω = 0.05 rps),產生的轉矩反而偏低。
這是什麼意思呢?你可以想像你在攪拌一碗綠豆,當你攪得越慢,遇到的抵抗卻越大;攪得越快,遇到的抵抗反而越小,聽起來是不是有點不合常理?
更奇怪的是,在兩種轉速之間,也就是中等轉速(Ω = 0.005 rps)的時候,轉矩出現了不規則劇烈起伏。從圖中的藍線可以看到,轉矩一次又一次的爬升、跌落、再爬升、再跌落,就像小型地震一樣,出現了大規模的「集體崩落」!
從鏡頭中看崩落現象
團隊在實驗時同步攝影,儀器每轉一定的角度(比如:每萬分之一圈),就將顆粒流的剖面擷取成影像。
實驗時容器內部剖面的圓球運動情況,顆粒軟球有加螢光染料顯影。資料來源│蔡日強
接著,將相片中每一格像素轉為對應數值,分別與上一時刻的照片相減,來得出顆粒體與上一時刻間的「差分影像」。
差分影像(State α):高轉速,承受轉矩小。其中:紅色表示顆粒由此側離開,藍色表示顆粒向此側接近。資料來源│蔡日強
差分影像(State T):中轉速,轉矩劇烈起伏,有集體崩落現象。其中:紅色表示顆粒由此側離開,藍色表示顆粒向此側接近。資料來源│蔡日強
差分影像(State β):低轉速,承受轉矩大。其中:紅色表示顆粒由此側離開,藍色表示顆粒向此側接近。資料來源│蔡日強
藉由這些時變圖,我們得以更明確地判讀顆粒體的運動方式,了解顆粒軟球位移的方向、快慢、範圍。從影像中可以看到,相較於高轉速與低轉速,在中等轉速時,確實出現了大規模顆粒球同時位移的現象,綜合以上的實驗數據和影像,團隊總結了幾個問題:
- 一般而言,流體在速度越快的時候,阻力會越大。然而在這次的實驗中,轉速越快、轉矩反而變小,跟過往認知不一樣。
- 中等轉速時,為何會出現集體崩落的現象?
- 有沒有什麼指標,可以預判集體崩落的出現?
這些問題,讓團隊當時感到十分頭痛,蔡日強回憶「剛開始我也覺得怪怪的,不過我們常說,如果你發現一件比較奇怪的事情,那只有兩種可能:一種是你弄錯了,另一種是真的有個新發現了!」
摩擦係數不是常數?
那麼,在顆粒流切變率加快的同時,究竟有什麼物理性質跟著改變了?
為了解決這些疑惑,團隊進行了許多獨立實驗。其中一個關鍵的實驗,就是量測顆粒軟球材質的「摩擦力」。他們採用同樣是 PDMS 材質的半圓柱棒,兩兩接觸並以不同切面速度(U)拖行,觀察過程中摩擦力的變化。
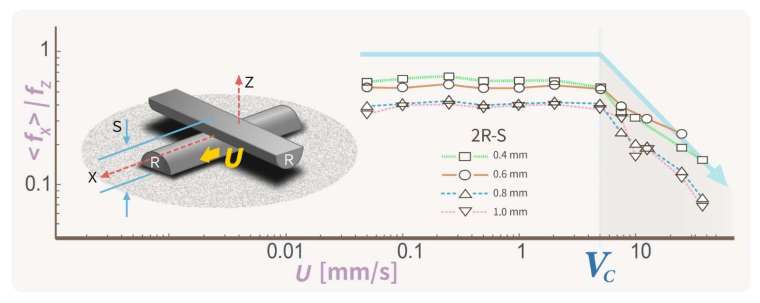
結果發現,當拖行速度較慢的時候,摩擦係數大約保持在定值,基本上就跟大家過往的認知一樣。但有趣的是,當速度超過一個臨界速度(VC)之後,摩擦係數卻像是坐溜滑梯一樣開始下降,換言之,顆粒軟球的表面突然「變滑了」。
從這個實驗可以確定,摩擦係數並非定值,而是會隨著速度增加而改變的數值。其實,「摩擦係數不是常數」的概念,並非什麼驚天動地的新發現,但過去許多顆粒流的研究,卻忽略了這個基本現象,只把摩擦力當成一般常數看待。
「摩擦係數不是常數」並非新觀念,但大家似乎都忘記這件事了。
而當我們把這個概念,重新應用在顆粒流實驗時,那些匪夷所思的現象,突然都有了合理的解釋!根據團隊的推測,當錐形圓盤轉速加快,快到一定程度的時候,有些顆粒軟球之間的速度,可能已經超過了 VC,導致顆粒軟球摩擦係數下降,才會讓量到的轉矩降低。而「集體崩落」的發生也可能是如此。
崩落現象的風向球:「slipperiness」
有沒有可能推估,顆粒流系統在受力之後,到底會偏向固體?流體?或是發生崩落現象呢?
為此,團隊創造了一個無因次量(不帶物理單位的參數),姑且稱為「slipperiness」,希望可以做為顆粒流行為的「預測指標」。
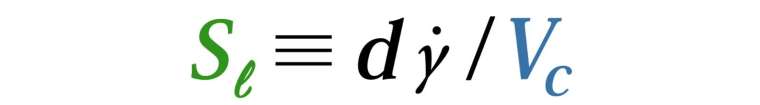
slipperiness 可以大略解讀成系統「平均而言有多滑」,代表了顆粒之間相對速度與臨界速度 VC 的大小關係,以及摩擦係數減損的程度。
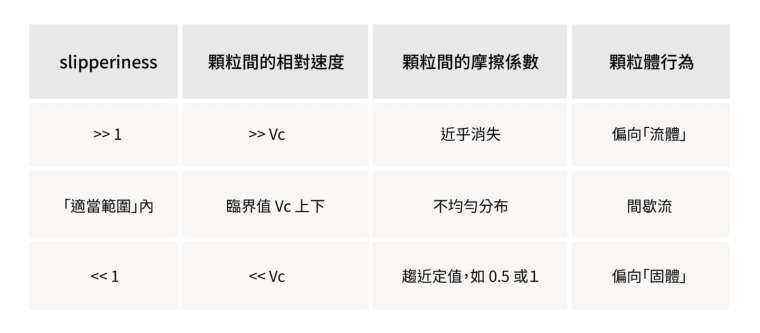
換言之,如果 slipperiness 遠大於 1 ,代表大部分顆粒體之間的速度大於 VC,摩擦係數近乎消失,難以構成橫向的受力,呈現幾乎「自由」的滑動,在這種情況下,顆粒體之間的液體成為阻力的主角,顆粒體的行為會比較偏向「流體」。
反之,如果 slipperiness 遠小於 1,顆粒體之間相對滑動即使有,速度也都不高,這種情況下摩擦係數接近定值,顆粒體之間可以很容易「消化」所有方向的力,扮演好整個系統承力的主角,顆粒體的行為會比較偏向「固體」。
然而,如果 slipperiness 剛好「不大不小」,代表這兩種極端情形有可能混搭,以局部或整體的方式交錯產生。最戲劇化的事件就會是前述的「集體崩落」,更正式的名稱可叫做「間歇流」。這危險區間的確切範圍,則有待更多細節來決定。
但有了 slipperiness ,蔡日強團隊至少搭出了第一座「橋梁」,連結過去難以相容的兩種觀點來看待顆粒流:一端是摩擦力完全沒打折,可視為「固體」(solid);另外一端,則是顆粒間摩擦力喪失殆盡,已經「完全液化」,可視為「流體」(fluid)。
然而,顆粒流的兩個極端之間其實有相當的過渡地帶,並不在原來習以為常的學術傳統裡。
雖然已發表的實驗還是非常簡化的版本,但蔡日強表示希望能透過論文提醒大家「摩擦力會改變」這件事,也希望拋磚引玉,「讓固體跟流體兩個學術社群,能夠有更多的對話」。
研究的下一步
現階段,團隊正著手改良實驗儀器並設計更多延伸實驗。舉例來說,如果顆粒軟球不一樣大,會發生什麼事?如果顆粒軟球不是圓球,行為會如何改變?如果軟球之間開始壓得不夠緊密的時候,「間歇流」的現象是否消失?這些問題,都是研究團隊接下來想了解的。

團隊也正積極透過電腦模擬,研究顆粒體在「無重力、無液體,僅考慮接觸力」的理想環境下,會有什麼樣的流動行為。
蔡日強說道「在實體實驗中,我們只有六個感測器可以推算顆粒流系統的受力反應,但在電腦模擬實驗中,等於有上千個感測器可以蒐集數據,真的是太棒了!」每一顆小球的受力、接觸、旋轉、位移等,在模擬中都看得一清二楚,讓團隊有機會作進一步的推論。
此為電腦模擬在中等轉速下的顆粒流變化。顆粒球之間的彈性能以顏色長棒標示,愈偏紅色那端、彈性能愈大、球和球之間愈緊;愈偏藍色那端、彈性能愈小、球和球之間愈鬆,顏色間的能量級距高達 10 的數次方 。影片中可以看到顆粒球發生集體崩落現象的「瞬間」,原本有很多紅橘色長棒,崩落之後幾乎都變成藍或綠,但長棒的數量只有些微增加,顯示彈性能隨著崩落事件大量釋放。
資料來源│蔡日強
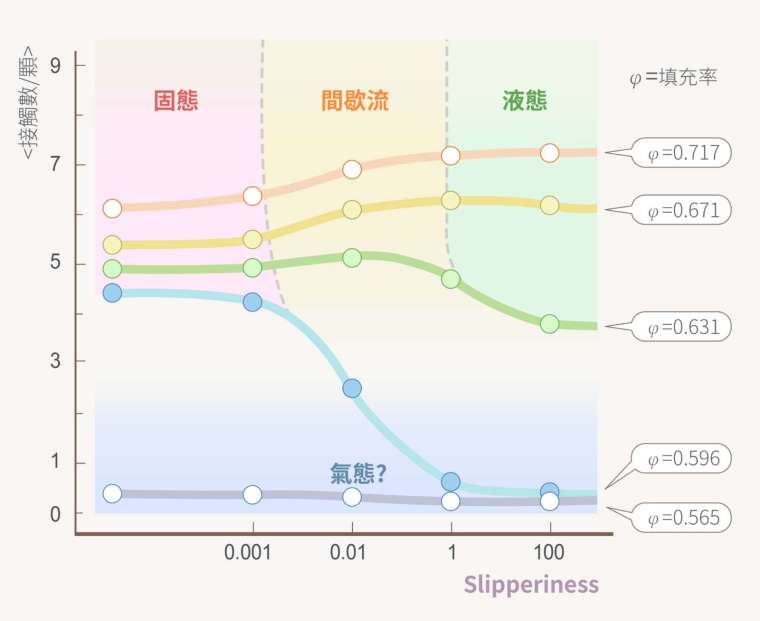
下圖是團隊正在統整的「三態圖」,顆粒流有三大區塊,分別是「固態」、「液態」,以及下方的「氣態(懸浮態)」。在緊壓(高密度、高壓力)的狀況下,固態和液態兩極端之間呈現一條「危險走廊」,可看到此案例在 slipperiness 介於 0.001 到 1 之間,發生集體崩落的現象。
不久之前,蔡日強也開始翻閱地震相關的書籍,想要了解顆粒流「集體崩落」的現象,與真正的地震和土石流,是否有可以互相參照的可能性?蔡日強的期待是讓「顆粒流研究」成為物理學家走入現實世界領域的另一個起點。
「我們離真正的戰場還很遠」,蔡日強笑著說:「但這一切,才正要開始!」

註 1:液體折射率和軟球一致是為了讓光線走直線,而不被球的表面偏折。這些膠球還會加上螢光染料,以便在光學攝影機下觀察。
註 2:切變率:在此指的是顆粒水平速度隨高度的變化率,更廣泛的定義參見延伸閱讀〈流沙、地震、土石,與沙漏裡的物理:「動靜之間」〉。
原文連結:
延伸閱讀:
- Tsai, J.-C., Huang, G.-H. and Tsai, C.-E. (2021). Signature of transition between granular solid and fluid: Rate-dependent stick slips in steady shearing. Physical Review Letters, 126, 128001.
- JC Tsai’s Lab: Ongoing Projects
- 蔡日強(2022)。〈流沙、地震、土石,與沙漏裡的物理:「動靜之間」〉,《物理雙月刊》。
- 顆粒流的展示影片(含「集體崩落」現象)